2023年8月22日,统计学大师C R Rao驾鹤西去,享年102岁。
Rao一生对数理统计学贡献卓著,发表了400多篇论文和14本统计学专著,在估值理论、统计推断、多元分析、信息几何学和计量经济学等方面的影响尤其深远。Rao最著名的发现包括Cramér–Rao界、Rao–Blackwell定理、Fisher–Rao定理、Rao距离和正交数组。他于今年早些时候刚刚获得了统计学界的最高奖项“国际统计学大奖”(International Prize in Statistics)。
至此,为20世纪统计学蓬勃发展作出巨大贡献,为经典数理统计学打下坚实数理基石的大师们都已凋零。他们亲手推动了数理统计学的发展,使之从一个数学的小分支,发展成为对各个科学技术领域全方位渗透的认知理念和技术手段。今天,统计学已经成为我们分析数据,理性决策的强有力的工具。今后,伴随着日益增长的算力,统计学也还将继续演进,成为数据科学和机器智能,也必将成为我们加速改变世界,探究洞悉宇宙本源不可或缺的理念和手段。
早期数据分析的出现(文明早期至 18 世纪)
早期帝国经常整理人口普查或记录各种商品的贸易。汉朝和罗马帝国是最早广泛收集帝国人口规模、地理面积和财富数据的国家。
“算术平均值”虽然是希腊人所熟知的概念,但直到16世纪才被推广到两个以上的值。Tycho Brahe首先在天文学中采用了这种方法,他试图用平均值的方法减少对各种天体位置估计中的误差。
“中位数”的概念起源于Edward Wright于1599年出版的导航书(《导航中的某些错误》)中有关用指南针确定位置的章节。Wright认为中位数是一系列观察中最有可能是正确的值。
“统计”一词是由意大利学者Girolamo Ghilini于1589年针对这门科学引入的。统计学的诞生通常可以追溯到1662年,当时John Graunt与William Petty开发了早期人类统计和人口普查方法,为现代人口学提供了框架。Graunt制作了第一个生命表,给出了每个年龄的生存概率。他的著作《对死亡率的自然和政治观察》利用对死亡率的分析,首次对伦敦人口进行了统计估计。他知道伦敦每年约有13,000场葬礼,每年每11个家庭就有3人死亡。他根据教区记录估计,平均家庭人数为8人,并计算出伦敦人口约为384,000人。这是比率估计方法的首次已知使用。
Abraham de Moivre于1733年左右开始了关于正态分布的研究工作,这为概率论奠定了基础,也对后来的数理统计推断至关重要。
概率论和数理统计的诞生(19世纪)
尽管统计方法在19世纪已扩展到科学或商业性质的许多领域,但是该学科的数学基础很大程度上借鉴了由Gerolamo Cardano、Pierre de Fermat和Blaise Pascal在16世纪开创的概率论。Christiaan Huygens在1657年对此主题给出了已知最早的科学处理。Jakob Bernoulli的《猜想的艺术》(在其死后9年的1713年出版)和Abraham de Moivre在1718年出版的《机会论》都将这一学科视为数学的一个分支。Bernoulli在他的书中提出了将完全确定性表示为1,将概率表示为0到1之间的数字的想法。
接下来,‘拉神’Laplace出场了,基本上以一己之力就把古典概率论打地基的活都干了。
Pierre-Simon Laplace在1774年首次尝试从概率论原理推导出观察组合的规则。他发现并指出,一旦忽略其符号,错误的频率可以表示为其大小的指数函数。该分布现在称为Laplace分布。Laplace还于1778年发表了他的第二误差定律,其中他指出误差的频率与其大小的平方的指数成正比。这就是现在最为人所知的是正态分布,它在统计学中具有核心重要性,因为它在自然发生的变量中频繁出现。1812年,Laplace发表了《概率分析理论》,建立了概率公理并引入了条件概率的概念,为统计学的数学基础做出了重大贡献。此书的前半部分涉及概率方法和问题,后半部分涉及统计方法和应用。到后来,人们才认识到Laplace误差理论与统计学的普遍相关性。
现代统计方法的发展(20世纪)
尽管统计理论的起源在于18世纪概率论的进步,但现代统计学只是在19世纪末和20世纪初才出现,许多具有严格数理统计意义的统计量和统计技术也在这个时期被定义、发明和完善。这一时期统计学的蓬勃发展分三个阶段。
第一波浪潮发生在世纪之交,由Francis Galton和Karl Pearson引领,他们将统计学转变为一门用于分析的严格数学学科,不仅在科学领域,而且在工业和政治领域也都找了广泛的应用。Francis Galton被认为是统计理论的主要创始人之一。他对该领域的贡献包括引入标准差、相关性、回归的概念,以及将这些方法应用于研究各种人类特征(身高、体重、睫毛长度等)。这方面的开创性工作为研究变量之间的关系奠定了基础。他还发现其中许多变量可以拟合正态曲线分布,这为现代回归分析铺平了道路。Karl Pearson强调科学规律的统计基础并促进了其研究。他的工作涵盖生物学、流行病学、人体测量学、医学和社会史领域。Pearson首先引入了相关系数的概念,发明了用于拟合样本分布的矩方法,他还创立了统计假设检验理论,Pearson的chi-方检验。
第二波数理统计浪潮由Ronald Fisher在1910年代和20年代开创。这涉及开发更好的实验模型设计、假设检验和用于小数据样本的估值技术。Fisher撰写了两本教科书:1925年出版的《研究人员的统计方法》和1935年出版的《实验设计》,这两本教科书定义了世界各地大学的统计学科的标准,在后来经历了多次版本和翻译,成为许多学科科学家的标准参考书。他还将之前的结果系统化,为它们奠定了坚实的数学基础。他首次使用了统计术语“方差”,首先引入了5% 的显著性水平。1930年,他出版了《自然选择的遗传理论》,将统计学应用于进化论。除了方差分析之外,Fisher还命名并推广了最大似然估计方法。Fisher还首创了充分性、辅助统计、Fisher线性判别子和Fisher信息的概念。
最后一波浪潮主要是对早期发展的完善和扩展,持续时间几十年。起始于于20世纪30年代Egon Pearson和Jerzy Neyman之间的合作。Egon Pearson(Karl的儿子)和 Jerzy Neyman 介绍了“II 型”错误、检验功效和置信区间的概念,彻底改变了基于样本数据做出统计决策的方式。Abraham Wald的序贯分析为自适应统计方法铺平了道路,在收集数据时实时优化决策。Harold Hotelling发展并完善了主成分分析,开始了多维统计量的统计方法。John von Neumann于1928年证明了极小极大定理。他后来改进并扩展了极小极大定理,将涉及不完美信息的博弈和两名以上玩家的博弈纳入其中,并在1944年与Oskar Morgenstern合著的《博弈与经济行为理论》中发表了这一结果,这也标志着博弈论这门新学科的诞生,为理性决策提供了数学分析的框架。
整个19世纪,Laplace在概率论方面的工作就是这一领域的天花板。直到一个世纪以后,由Andrey Kolmogorov领军的莫斯科学派通过公理化方法为概率论提供了严格的基础,统一了概率论的各个方面,结束了数学界近三个世纪有关精确的概率定义的各种争议。从基本公理出发的方式与欧几里得几何学的处理方式相当。Kolmogorov在他的经典著作《概率论基础》中严格地建立了概率论,并给出了条件期望的严格定义。在他1938年发表的论文“概率论中的分析方法”中严格定义了马尔可夫链。这些为后来Norbert Wiener,Joseph Doob,钟开莱等研究随机过程、布朗运动奠定了基础。
统计计算和数据科学的出现(20 世纪后期至今)
20世纪后期,计算能力的激增导致计算统计的兴起,使得人们越来越普遍地使用复杂算法和统计模拟技术来分析大型数据集,解决更多用传统方法无法解决的科学、工程和人文领域的问题。这些统计计算方法的出发点深植于概率论和数理统计原理,其逼近和收敛的机制都有别于传统的数值计算方法。
蒙特卡罗方法的早期变体被设计来解决Buffon的针问题,通过将针落在由平行等距条带制成的地板上来估计π的值。20世纪30年代,Enrico Fermi在研究中子扩散时首次尝试了蒙特卡罗方法,但他并没有公开发表这项工作。20世纪40年代末,Stanislaw Ulam在洛斯阿拉莫斯国家实验室从事核武器项目时发明了马尔可夫链蒙特卡罗方法,他和von Neumann一起设计了算法。
1949年Maurice Quenouille开发了折叠刀技术(jackknife),并于1956年进行了完善。这是一种重采样形式,它对于偏差和方差估计特别有用。John Tukey于 1958年扩展了该技术,并使用了“jackknife”这个名称,意即它是一个粗糙且现成的工具,可以较低的抽样和计算成本,获得还算可以的逼近效果。在jackknife技术的基础上,Bradley Efron在70年代到80年代发展了一整套的Boostrap技术和工具。该技术允许使用随机抽样方法估计几乎任何统计数据的总体分布。Bootstrap的一大优点是它的简单性。这是一种导出复杂分布估计量(例如百分位数、比例、优势比和相关系数)的标准误差和置信区间估计值的直接方法。
1977年Arthur Dempster、Nan Laird和Donald Rubin 发表了一篇论文对期望最大化(EM)算法进行了解释并命名。EM算法是一种迭代方法,用于查找统计模型中参数的局部最大似然或最大后验 (MAP) 估计,其中模型取决于未观察到的潜在变量。EM算法用于在无法直接求解方程的情况下查找统计模型的局部最大似然参数,大大扩展了最大似然法的应用范围。之前有统计学者在一些特殊情况下多次使用了某种形式的EM算法,D-L-R论文全面概括了该方法,并为更广泛的问题概述了收敛分析,将 EM方法确立为统计分析的重要工具。(该文对算法的收敛分析存在缺陷,吴建福于1983年发表了正确的收敛分析并拓展了EM方法的收敛范围。)
随着算力的继续爆发,算力成本不断下降,基于各种回归分析的预测建模、决策树、聚类、分类等机器学习技术的出现进一步扩展了统计学的边界,逐渐形成数据科学这一跨学科领域。数据科学意欲通过统计技术和计算工具相结合从各种大量数据中快速提取有效的知识和模式特征,进而形成更优化的认知模型和决策过程。
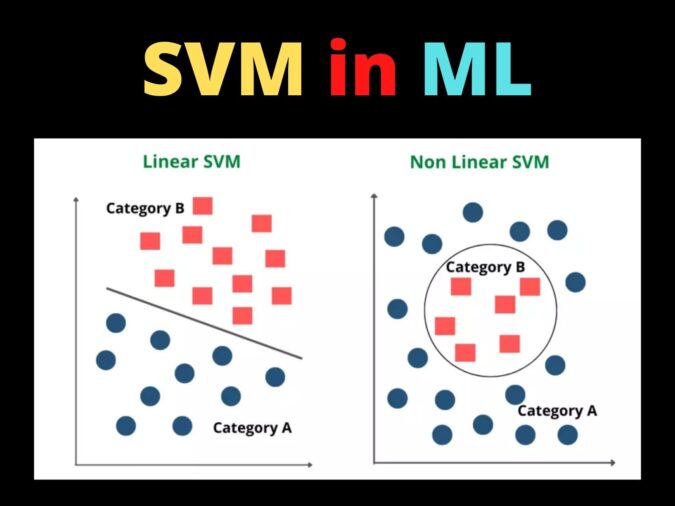
1992年Bernhard Boser、Isabella Guyon和 Vladimir Vapnik等提出了支持向量机(Support Vector Machines – SVM),这是基于Alexey Chervonenkis在1974年提出的统计学习框架。SVM算法可用于分类和回归的监督学习模型,可分析数据以进行分类和回归分析的预测,其优势是具有相当的稳健性。
1995年何天琴使用随机子空间方法创建了第一个随机决策森林算法(Random Decision Forests),2001年Leo Breiman和 Adele Cutler扩展了该算法。随机决策森林是一种用于分类、回归和其他任务的集成学习方法,通过在训练时构建大量决策树来进行操作。随机决策森林纠正了一般决策树过度拟合训练集的倾向,因此通常优于决策树算法。
1999年Jerome Friedman开发了显式回归梯度提升算法(Gradient Boosting),同时Llew Mason、Jonathan Baxter、Peter Bartlett和Marcus Frean 提出了更通用的函数梯度提升观点。梯度提升是通过迭代选择指向负梯度方向的函数来优化函数空间上的成本函数的算法。这种提升函数梯度观点导致了提升算法在回归和分类之外的机器学习和统计的许多领域的发展。
在过去几十年里,深度学习技术也取得了重大突破,并催生了一些新的机器学习算法。
福岛邦彦受到神经科学家在对猫视觉的研究成果的启发,在80年代提出卷积神经网络(CNN)的初始模型,一种正则化类型的前馈神经网络,它通过过滤器(或内核)优化自行学习数据特征。这种模型被后来的学者不断的优化和拓展,在图像处理和计算机视觉中获得了广泛的应用,在近来更成为深度学习领域的主要工具和框架。
另一大类型人工神经网络是循环神经网络(RNN)。与CNN这样的单向前馈神经网络不同,RNN是一种双向人工神经网络,允许某些节点的输出影响相同节点的后续输入。1989年,Yann LeCun首次将卷积神经网络与反向传播结合起来提高图像识别的准确度。1990年,Jeffrey Elman提出了RNN算法。1997年,Sepp Hochreiter和Juergen Schmidhuber开发了用于RNN的长短期记忆(LSTM)。2015年,何恺明、孙剑、任少卿、张祥雨提出了残差网络(ResNet),使得具有数十或数百层的深度学习模型能够轻松训练,并在更深入时达到更高的准确性。
2014年Ian Goodfellow等人于提出生成对抗网络(GAN)。GAN的核心思想是通过生成器和判别器的之间的对抗训练,使得模型能够以无监督的方式学习。GAN类似于进化生物学中的模仿进化的竞赛,是这一波生成型AI热潮的主要技术推力。
2014年,Dzmitry Bahdanau、Kyunghyun Cho和Yoshua Bengio提出了用于机器翻译的注意力机制。2017年Google Brain团队发布的论文“Attention Is All You Need”提出了Transformer,一种依赖于并行多头注意力机制的深度学习架构。它比以前的循环神经架构(例如LSTM)需要更少的训练时间。这种架构现在不仅用于自然语言处理和计算机视觉,还用于音频和多模态处理。其后来的变体已普遍用于在大型语言数据集上训练大型语言模型,如GPT和BERT。它还促进了预训练系统的发展,例如生成式预训练模型GPT, PaLM, LLaMA等。
深度学习技术的研究和开发还在如火如荼地进行,这项技术的应用不仅在各个领域不断地渗透和扩展,而且许多人相信这可能是最终通向通用人工智能(AGI)的路径。我们日常许多场景里,机器预测和认知的能力在不断提高,由点及面会逐步超越我们的水平。我们一度曾经引以为傲的复杂认知能力,也将不会是地球上的唯一。认知能力不断提高,成本不断下降,而且可以大规模地应用,大范围内分发,这就是机器智能突破的本质所在。
C R Rao的“三句偈”
C R Rao在他百岁生日接受采访时说出了掷地有声的“三句偈”,道出了他以一个多世纪的阅历对人类认知的深刻洞察,和对他自己参与创立的数理统计学的信心和雄心。
All knowledge is, in the final analysis, history.
All sciences are, in the abstract, mathematics.
All methods of acquiring knowledge, are essentially statistics.
意即:
在终极的分析中,一切知识都是历史;
在抽象的意义下,一切科学都是数学;
所有获取知识的方法,本质上都是统计学。
“统计”一词原意指的是各国系统性地收集人口和经济数据。自文明诞生以来,统计的基本手段就已被使用。经过几个世纪的演进,特别是20世纪一众杰出数理统计学家的努力,统计学逐渐成为我们分析数据,理性决策的强有力的工具。不仅在应用广度上已经有迈越数学、物理等基础学科的趋势,而且在深度上也足以比肩。概率统计学的认识论和方法论越来越对数学物理代表的确定论和因果论形成不可或缺的补充和延展。这也是Rao“三句偈”的底气所在。
随着机器预测和认知能力的不断提高,由点及面地逐步超越我们的水平。我们一度曾经引以为傲的复杂认知能力,也将不会是地球上的唯一。所谓的知识表达,也不一定非要只适合人类的认知能力。在这个意义下,我们认为Rao的“三句偈”中,最先被动摇的可能是第二句:“在抽象的意义下,一切科学都是数学”。