Paul Erdős(1913年-1996年),匈牙利籍犹太人。1913 年 3 月 26 日出生于匈牙利布达佩斯,是一位才华横溢、极其高产的数学家。他对数学有着无与伦比的热爱,一生专注数学,心无旁骛,以不懈的热情追求数学。他在数论、组合数学和图论等数学领域做出了广泛的贡献,对其几个主要分支的发展起到了核心作用,影响力深远。他是人类有史以来最高产的数学家。从1932年发表第一篇论文开始,直到在他去世7年后的2003年,依旧有零星的论文陆续发表。他一生发表论文高达1525篇(包括与人合写的),以平均每年发表20多篇论文的速度在产出,是到现时为止发表论文数最多的数学家,甚至超越了位列高产第二的‘数学皇帝’欧拉。Erdős除了他本身就是一位卓越多产的数学探索者,也通过以他为中心的数学研究合作形成巨大网络。他曾和500多人合写论文,在数学界有一个很有趣而有意义的指标,叫Erdős数,用于衡量一位数学家和Erdős合作的紧密程度,象征着数学界的合作和互联互通。
Erdős游牧生活方式与他的数学工作一样独特。他一生过着居无定所的生活,没有固定的工作,只带着两只半空的手提箱周游世界。他从一个大学到另一个大学,从一个国家到另一个国家,从一个数学家到另一个数学家,不知疲倦地与其他数学家合作。他经常同时与多达十几位数学家合作研究不同的课题,游刃有余地在不同的数学问题之间转换移动。这种生活方式不仅培养了数学界的社区意识,还让他能够分享想法并激励他人。
Erdős的才华和高产,他在离散型数学分支领域开拓性的贡献和深远影响力,他对数学研究和合作的推动,使他成为数学界的传奇人物。
生平: 从神童到流浪数学大师
Erdős遗传了来自数学教师父母优异的基因,是一个神童,从小就表现出非凡的数学天赋。三岁时就能轻松心算一个人一生所活的秒数,并经常在客人面前表演四位数的乘法心算。他在四岁时独立形成了“负数”的概念。“我告诉妈妈,”他说,“如果从 100 中减去 250,结果会是 -150。”在Erdős出生前不久,他的两个姐姐都因得猩红热而夭折,因此他的母亲一生都对他保护有加。她没有让Erdős去上公立学校,而是为他聘请了一位私人教师,让他在家完成了整个初等教育。16 岁时,父亲给他介绍了两门他一生都喜欢的学科——无穷级数和集合论。高中时,Erdős热衷于解决每月在《中学数学和物理杂志》上出现的数学问题。当时匈牙利有明确的歧视政策,凡被认定为犹太人的人不得进入大学系统,Erdős直到 1930 年才因为在全国统考中成绩优异而被特批进入大学。四年后,年仅二十一岁的他即被布达佩斯大学授予数学博士学位,师从数学家Leopold Fejer(他也是John von Neumann的导师)。他于 1934 年获得博士学位后即离开匈牙利,前往英国曼彻斯特大学攻读博士后。此后,Erdős还在剑桥、伦敦、布里斯托尔等地工作过。在剑桥大学期间,Erdős结识了著名的数学家G.H. Hardy和Stanislaw Ulam。
1938 年,由于希特勒控制了奥匈帝国,他无法再安全地返回匈牙利,因此Erdős决定接受普林斯顿高等研究院为他提供的为期一年的任命。尽管Erdős在期间取得了很不错的研究成果,然而一年任期结束后,普林斯顿高研院拒绝续签他的任期;普林斯顿认为他“粗鲁且不合常规” ,并提出只延长他的任期六个月。Erdős于是离开了普林斯顿,开始四处游荡,从一个大学到另一个大学,但他拒绝了全职工作机会,这样他就可以自由地与任何人在任何时间解决他选择的任何问题。
1941 年,Erdős和另外两名数学家在散步时忽略了“禁止擅闯”标志,心不在焉地走进了在长岛的一个军用秘密雷达基地。一名基地警卫拦截了他们,对他们进行盘问后觉得他们并无恶意,就让他们平和地离开了。警卫事后又认为他们的行为有些古怪,就向上报告了这一事件,FBI后来就此事询问了这两位数学家。这导致Erdős被 FBI 立了档案,也为他后来引来了不少的麻烦。
1943 年,Ulam试图让Erdős为美国政府在洛斯阿拉莫斯的核武器项目工作。Erdős有兴趣参与该项目(并帮助摧毁控制整个东欧的法西斯政府),但他在安全面试中不够谨慎和通融,甚至在公共场合大声询问“原子弹的研制进展如何?”,以致激怒了军事安全人员。Erdős因此失去了资格,没有被批准加入政府的核武器项目。Erdős就去普渡大学做了一份兼职工作。
由于匈牙利在二战中与德国结盟,在美国的Erdős一度好多年失去了与在匈牙利家人的联系。1945 年,苏联军队解放了布达佩斯。Erdős此时才得知,他的大家庭中的大部分成员都在奥斯维辛集中营被杀害,只有他母亲和一个堂妹幸存。而Erdős的父亲已在 1942 年死于心脏病。Erdős在1948年回到了匈牙利,并花了大量时间往返于英国和美国之间。1952 年圣母大学给Erdős提供了一个很特殊的的临时职位,让Erdős可以完全自由地随时地去进行一些合作研究。Erdős欣然赴任。
20 世纪 50 年代初,参议员McCarthy开始在美国煽动强烈的反共情绪,来自匈牙利的Erdős开始受到美国当局的怀疑。1954 年,Erdős在欧洲参加完会议后回国,美国移民局拒绝为Erdős签发入境签证,理由是Erdős在FBI留有案底。以致Erdős在 20 世纪 50 年代的大部分时间都在以色列度过。结果出现了一种模式,美国国务院拒绝签发入境签证,然后国际数学界会散发一份请愿书,要求Erdős参加某个特定的学术会议。有时国务院会在有限的时间内让步,但大多数情况下他们不会让步。这种情况一直持续到 1963 年 11 月,他才又获得了美国的长期签证。
Erdős也开始了近半个世纪的流浪生活,没有固定的住所,没有妻子,没有值得牵挂的财产,也没有工作束缚他,只拎着两只半空的手提箱,在世界各地游荡。他的流浪癖把他带到了以色列、中国、澳大利亚和其他 22 个国家。Erdős从来不关心自己的日常生活,也没有真正掌握大多数人认为理所当然的生活自理技能。他不必做饭、打扫卫生或完成任何其他可能耗费他投入到数学中的时间和精力的日常任务。他一般就住在一个合作者的家里,只要他的合作者提出有趣的数学挑战,并能照顾他的生活起居,他就会一直待在那里。一直工作到他的合作者筋疲力尽,然后继续前进到下一站,指引他的只能是下一个需要解决的数学问题。
Erdős一生完全献给了数学。除了数学互动之外,他几乎没有什么人际关系。事实上,他都不一定知道他的一些长期合作者的基本信息,包括他们的名字。他能记住几乎每个数学家的电话号码,但他往往不能匹配任何人的名字。由于Erdős的许多合作都是通过邮件进行的,而且由于他与很多人打交道,他常常会忘记他们实际上长什么样。有一次,Erdős遇到了一位数学家,问他来自哪里。“温哥华,”数学家回答道。“哦,那你一定认识我的好朋友Elliot Mendelson,”Erdős说。回答是“我就是你的好朋友Elliot Mendelson。”
在1971年他的母亲去世后,Erdős失去了这个世界上唯一深爱的亲人,这种伤感在他身上持续了很多年。他开始服用大量抗抑郁药,后来又服用安非他明。除了每天大量的咖啡,Erdős也大量使用其他的兴奋剂。Erdős试图通过埋头研究数学来恢复生活中的某种平衡,他每天坚持花 19 个小时进行数学研究。Erdős的朋友们担心他染上毒瘾不能自拔。1979 年,老朋友Graham和Erdős打赌 500 美元,说他一个月都停不下服用安非他明。Erdős接受了赌局,并彻底戒掉了一个月。Erdős在月底的评论是:“你向我证明了我不是瘾君子。但我没有完成任何工作。我早上起床时盯着一张白纸。我没有任何想法,就像一个普通人一样。你让数学的发展倒退了一个月。”然后他立即又开始服用安非他明。
Erdős还积极寻找年轻的天才,并与他们合作。他通常能够引导他们成为数学界的中坚力量,著名数学天才陶哲轩就是其中之一,在很小的时候就接受过他的指点。Erdős通过演讲费、奖金和兼职工作获得的钱通常捐赠给无家可归的人、慈善机构和有抱负的研究人员。他曾经给一位为支付哈佛大学学费而苦苦挣扎的高中生 1,000 美元。十年后,那名学生想把这笔钱还回去,Erdős告诉他说,“用这一千美元去做我做过的事吧。”
Erdős一生获得了至少 15 个荣誉博士学位。他成为八个国家的科学院院士,包括匈牙利科学院院士 (1956 年)、荷兰皇家艺术与科学学院的外籍院士(1977 年)、美国国家科学院院士 (1979 年) 和英国皇家学会院士 (1989 年)。1983 年,他和陈省身分享了数学界最高也是奖金最丰厚的奖项——Wolf奖,他将 5万美元奖金中除 720 美元外的所有奖金都用于在以色列设立奖学金,以纪念他的父母。
Erdős打破了数学是年轻人的游戏这一传统观念,在80岁以后,仍然每天工作十几小时,一直坚持数学证明和猜想。在他生命的最后阶段,Erdős觉得他的数学能力开始下降,因为他开始难以理解 40 年前他在论文中使用的论据。他开始让 Graham 来检查他的工作;Graham 报告说,他通常仍然不会犯错误。1996 年 3 月,Erdős在演讲时失去了知觉。不久后恢复意识,他要求听众不要离开,并坚持说:“我还有两个问题要告诉他们”。1996 年 6 月,Erdős参加了一次会议,在听演讲结束时,Erdős开始提问,但在演讲者回答完问题之前就失去了意识。他被紧急送往手术室并植入了心脏起搏器。1996年9 月 20 日,83 岁的Erdős在华沙的一次会议上解决了一个棘手的几何问题后仅几个小时就因心脏病发作去世。他的葬礼在布达佩斯举行。Erdős的追悼会上出席人数超过 500 人。Erdős的遗体被火化,并被埋葬在他一生挚爱的母亲遗体旁边。
数学成就和历史定位
Erdős在大学一年级的时候给出了一个Bertrand猜想的新证明。Bertrand猜想于 1850 年首次由Chebyshev证明。Chebyshev的证明非常冗长且复杂,并且被认为不是特别优雅。后来Ramanujan给了一个比较简洁的证明。而Erdős只用了初等数学的方法给出了一个更加优雅的证明。这篇发表于1932年的论文是Erdős平生发表的第一篇数学论文,以其简洁和优雅震惊了国际数学界。它也让世界首次领略了一种后来与Erdős密不可分的证明风格。Erdős 一早就显示了非常强烈的数学美学意识,这强烈影响了他的所有工作。他不只是想要一个解决方案;他想要一个将看似不同的概念联系在一起的优雅解决方案。这种数学美学的感觉对 Erdős 来说几乎具有宗教意义。
1935 年Erdős和Szekeres 合作证明了后来以他们名字命名的定理,指出平面中任何足够大的点集都包含凸位置的大子集或凹位置的大子集,这是 Ramsey 理论应用于几何学的一个基本结果。
在普林斯顿高研院期间,他开始在‘数学年鉴’等顶流学术期刊上发表论文。他和Hurewicz合作了一篇有关维度论的文章,解决了Hilbert空间中有理点集的维度问题。这是一个他之前几乎一无所知的领域,他在了解了一些基本概念和定义后没有多久就给出了答案。他因此被认为是第一个给出非零维的完全不连通拓扑空间的例子的人。在拓扑学里,这类空间即被冠以Erdős空间。他也和Turán合作了有关近似论的论文,并与Kac和Winter共同创立了概率数论领域。
1948年,Erdős在素数问题上取得了不错的成果。他和Selberg用初等数学的方法证明了素数定理(该定理是关于素数在越来越大的数字中出现的频率的陈述)。Selberg 的一位同事向 Erdős 描述了一些最近的进展,他很快就在证明的某个特定部分超越了 Selberg,最终得出了素数定理的证明。Selberg对Erdős 不请自来的参与感到不满,他迅速开发出不依赖Erdős 方法的替代版本证明,并随后因该项成果以及其他有关素数筛选法的成果,获得了1950年的Fields奖。1951 年,同门师兄von Neumann为Erdős在素数理论方面的工作颁发了Cole奖。
此后,数论一直是他感兴趣的领域之一。他研究了数论的各个方面,包括丢番图问题、加法数论、素数分布、序列的可分性、多项式和基数。1975年,Erdős和Selfridge合作解决了一个 150 年前的难题,证明两个或多个连续正整数的乘积永远不会是平方数、立方数或任何更高的幂。
图论是另一个Erdős做出极大贡献的数学分支。如果说欧拉是图论的创始鼻祖,那Erdős可以称得上是推动图论成为内容丰富的数学分支最重要的推手。1959 年,Erdős参加了第一届国际图论会议。他在图论方面的主要贡献是开创了随机图论和极值图论两个子领域。他与 Rényi 一起开发了随机图理论,建立了Erdős-Rényi 模型,并引入了图属性中急剧“相变”的概念 。Erdős在建立极值图理论的努力中同样做出了重大贡献,该领域试图探究图参数变化如何影响图属性。随着网络在我们的生活和产业中日益普及,图论的重要性也越发凸显。图论不仅推动了对复杂网络系统的理解,也为分析网络性能和优化网络结构提供了强大的工具。
在与图论有密切关系的另一个数学分支,组合数学中,Erdős对Ramsey理论的发展作出了突出的贡献。他也是第一个充分认识到随机方法强大威力的人,并将其成功引入到组合数学的应用中,这种概率论方法被称为“Erdős方法”,被广泛认为是在寻求存在性证明时非常有效的工具。极值组合学的整个方法也要归功于他,部分源自传统的解析数论。在50年代到60年代,他和合作者Rado和Hajnal陆续发表的三篇论文奠定了分割理论的基础。
此外,他还在集合论、几何学、分析学等方面做出重要贡献。他所涉猎数学领域的多样性非同寻常。根据数学家George Purdy回忆,1976 年,他和Erdős在德克萨斯 A&M 大学的数学休息室喝咖啡。黑板上写着一个函数分析问题,而 Erdős 对这个领域几乎一无所知。而Purdy碰巧知道,两位分析学家刚刚给出了一个长达 30 页的解来解决这个问题,他们对此感到非常自豪。Erdős 抬头看着黑板说:‘这是什么?是一个问题吗?’得到肯定答复的他走到黑板前,眯着眼睛看着简洁的陈述。他问了几个关于符号代表什么的问题,然后就毫不费力地写下了一个两行的解决方案。
除了等身的论文著作,Erdős还通过他留下的许多数学猜想传承他的思想和遗产。在数学中最难的事情往往是提出正确的问题,而他却非常善于指出重要问题。就像上个世纪初,Hilbert提出的23个数学问题极大影响了整个世纪的数学发展,即便在当今也还有影响力。Erdős提出的猜想也将影响着他身后的数学发展。Erdős也为一系列他无法解决的数学问题设立了奖项。他根据自己对问题难度的估计来设定奖金水平。奖金数额在 1 美元到 1,000 美元之间。其中一些问题仍然悬而未决,奖金由Erdős的遗产和其他相关方提供。
毫无疑问,Erdős是本世纪最伟大的数学家之一,他也是历史上最多产的数学家之一。他提出并解决了许多组合数学和其他领域的棘手问题,大大拓展了我们对离散型数学领域的认知边界,这是计算机和网络科学发展的基础。终其一生的数学风格,Erdős更像是一个“问题解决者”,而不是“理论开发者”。数学家Joel Spencer表示,“Erdős在 20 世纪数学殿堂中的地位存在一些争议,因为在他辉煌的职业生涯中,他一直专注于特定的定理和猜想。”Fields奖获得者Tim Gowers在他的《数学的两种文化》一文中有关于这两种风格的深入讨论,以及为什么问题解决者可能在当今数学界不太受重视的历史原因。Erdős一生专注离散型的数学领域,相较于更传统的分析学、几何学等连续统领域,恰恰是人类到目前为止理解得少而浅的。其许多研究对象都有其独特性,还很难形成统一的理论框架。也许我们也更应该感到庆幸有Erdős这样的天才出现,他像一个钻石挖矿人,向我们展示一颗颗来自数学宝库的零星宝物,其后可能隐藏着更大的宝藏。随着计算机和网络技术的发展,Erdős对人类知识库的贡献和价值也会随着时间的推移而更加凸显出来。
Erdős数
Erdős一生与 500多位作者合作过,几乎是第二位人脉最广的数学家的两倍。Erdős的合作如此之多,以至于在数学界形成一个独特而又广为接受的衡量指标,即数学家的“Erdős数”,来衡量一位数学家和Erdős合作的紧密程度。Erdős自己的Erdős数为 0。与Erdős合著论文的 509 位幸运数学家的Erdős数为 1。与该群体中的一位(但不是Erdős本人)合著文章的数学家的Erdős数为 2,依此类推。如果从一个人到Erdős没有论文链接路径,那么这个人的Erdős数就是无限的。Erdős数的分布如下:
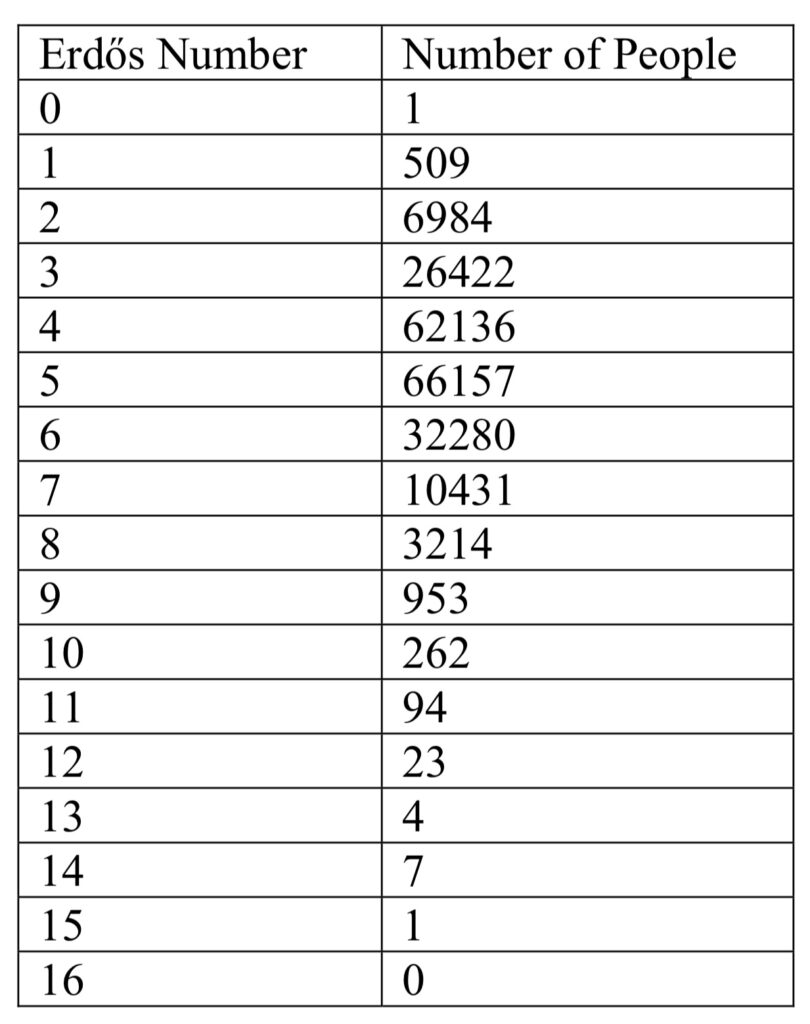
有好事者投入了惊人的精力来研究Erdős数,既是为了消遣,也是为了理解作者网络中的连接模式。以下是一些有趣的事实:
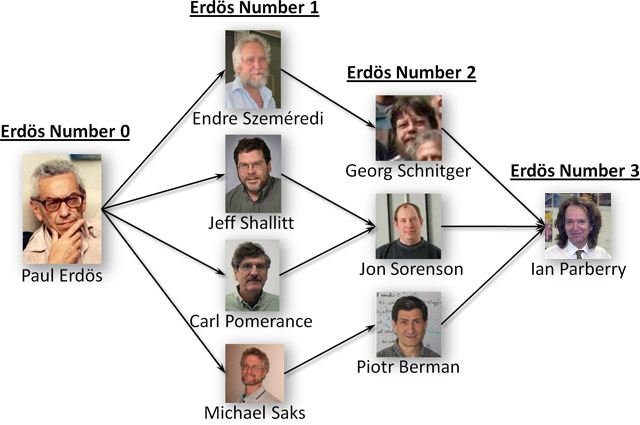
在与Erdős共享作者链的250,000多名数学家中,其Erdős数中位数是五。平均值为 4.69,标准差为 1.27。钟开莱曾经与Erdős合作发过论文,他的Erdős数是1。其余几位著名的华裔数学家陈省身、丘成桐、陶哲轩的Erdős数都是2。已知在职数学家的最高Erdős数是 7。笔者在念研究生时的两位导师的Erdős数都为3。随着时间的推移,Erdős数的整体分布会慢慢向上移动。
有人曾试图在 eBay 上出售Erdős数。获胜者将有机会与卖家合作,卖家的Erdős数为 4。有几个人出价很高,但拍卖在最后一秒被一位无意付款的数学家以 1,031 美元的价格抢走,他称这一噱头是对Erdős数的“嘲弄”。
许多数学界以外的知名人物也都有Erdős数:例如爱因斯坦的Erdős数是 2;杨振宁的Erdős数是 3;李政道的Erdős数是 4;德国前总理Angela Merkel曾是物理学家,她的Erdős数是5;物理学家Stephen Hawking的Erdős数是4;Elon Musk的Erdős数是4;现代语言学之父Noam Chomsky的Erdős数是4。奥斯卡最佳女主角奖得主Natalie Portman 因本科时发表的神经科学论文(以她的本名娜塔莉·赫什拉格 (Natalie Hershlag) 发表)而拥有Erdős数 5 。
想知道自己或其他人的Erdős数吗?在美国数学协会网站可以查阅:https://mathscinet.ams.org/mathscinet/freetools/collab-dist





